Waves
The disturbance which propagates from one point to another point without net transport of matter is called wave. It is due to repeated simple harmonic motion of particle carrying energy but not due to actual linear movement of particle carrying energy.
Examples: sound wave, light wave, water ripples etc.
Characteristics of Wave Motions:
- Wave motion is a disturbance propagating in a medium.
- It transfers energy as well as momentum from one point to another.
- When it propagates in a medium particles of the medium execute vibrating
- motion about their mean position.
- It has finite and fixed speed which depends on the nature of the medium and
- is given by v = 𝑓 × 𝜆.
- 5. Speed of wave and particle velocity are different. The particle velocity is 𝑣 =𝑎𝜔𝑐𝑜𝑠𝜔𝑡.
Types of wave motion
1. Electromagnetic waves
2.Mechanical waves
3.Matter waves
Electromagnetic waves
1. Doesn't need a medium for its propagation. light wave,
heat waves, radio waves etc.
2. Speed is equal to speed of light.
3. Moving charges back and forth will produce oscillating
electric and magnetic fields. The electric field and magnetic field are
perpendicular to each other.
Mechanical waves:
• Requires material medium for their propagation.
• For the propagation of mechanical waves, medium must possess
elasticity, inertia and low resistance for motion (i.e. damping must be very
small)
• Examples: water waves, sound waves, waves in pipes and strings
etc.
Types of mechanical waves
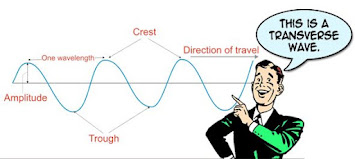
Transverse waves:
• Vibration is perpendicular to the propagation of waves.
• For the propagation of transverse wave medium should havemodulus
or rigidity. So, these waves are present in solids.
• Polarization is possible.
• Travels in the form of crest and troughs.
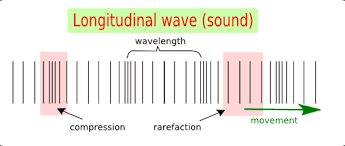
Longitudinal waves:
• Vibration is parallel to the propagation of waves.
• For the propagation of longitudinal waves medium must have
Bulk modulus of elasticity. So, these waves are present in all three media
solid liquid and gases.
• Polarization is not possible.
• Travels in the form of compression and rarefactions.
Matter Wave
The waves associated with the microscopic particles such as electrons, protons, neutrons, atoms and molecules when they are in motion are called matter waves. The concept of matter wave was first introduced by de-Broglie, so it is called de-Broglie wave
Waves on the water:
Water waves are an example of waves that involve a combination of both longitudinal and transverse motions. As a wave travels through the water, the particles travel in clockwise circles. The radius of the circles decreases as the depth into the water increases.
Notes: Waves on the earth surface during earthquake is the combination of longitudinal and transverse waves.
Some terms related to wave:
Displacement:
The distance of an oscillating particle of the wave from its
equilibrium position at any particular time.
The displacement equation is,
𝒚 = 𝐚𝐬𝐢𝐧
𝒘𝒕
− 𝜱
Where, y= displacement of the particle at any instant of
time ‘t’
a= amplitude=maximum displacement from its mean position.
w= angular frequency=2𝜋𝑓
𝑤𝑡 − 𝛷=phase of the wave
Particle speed:
During wave propagation medium of the particles undergo
simple harmonic motion
around their mean position. The speed of these particles is called particle speed.
We know,
𝒚 = 𝐚𝐬𝐢𝐧(𝒘𝒕 − 𝜱)
Differentiating with respect to time we get,
𝑎𝑤𝑐𝑜𝑠(𝒘𝒕 − 𝜱)
∴ 𝒗 = 𝒂𝒘𝒄𝒐𝒔 𝒘𝒕 − 𝜱
For maximum speed, 𝑐𝑜𝑠(𝒘𝒕 − 𝜱) =1 so = 𝑎𝑤 (𝑚𝑒𝑎𝑛 𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛)
For minimum speed. 𝑐𝑜𝑠 (𝒘𝒕 − 𝜱) =0, so = 0 (𝑒𝑥𝑡𝑟𝑒𝑚𝑒 𝑝𝑜𝑠𝑖𝑡𝑖𝑜𝑛)
Frequency:
Number of complete oscillation made by oscillating particles in one second is called
frequency. It is denoted by ‘f’. Its SI unit is Hertz(per second).
Wavelength
The distance between successive identical parts of the wave. It's unit is meters. Also,
The linear distance travelled by wave in one complete oscillation is called wavelength.
Time period
The time taken for one complete oscillation is called time period.
It is denoted by T
Or,
It is also defined as the reciprocal of frequency.
i.e.
Its SI unit is seconds(s)
Wave Velocity
Linear distance travelled by wave per unit time is called wave velocity.
i.e. 𝑤𝑎𝑣𝑒 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 = 𝑤𝑎𝑣𝑒 𝑙𝑒𝑛𝑔𝑡ℎ / 𝑡𝑖𝑚𝑒 𝑝𝑒𝑟𝑖𝑜𝑑
∴ 𝑣 = 𝜆 × 𝑓
Its SI unit is
Phase of the wave:
The argument of the sine/cosine in a given wave equation is called phase angle or simply phase of the wave. It gives the state of the vibrating particle as regards its position and direction of motion.
The equation of progressive wave is,
Here, phase of the wave(𝜑) =
Its SI unit is radian.
Progressive Waves
The waves which moves in forward direction with constant amplitude is called progressive waves.
Characteristics of Progressive Waves:
- A progressive waves transfer energy from one part of space at other
- In progressive waves, no particle is permanently at rest.
- In progressive waves all the particles vibrates with same amplitude and with same frequency.
- It may be either transverse or longitudinal.
Equation of progressive waves and equation of stationery wave equation:
From Book
Principle of superposition of waves.
The principle of superposition of waves state, "if two or more that two waves superimposed, then the displacement equation of the resultant waves is equal to the algebraic sum of the displacement of the individual waves that superimposed.
Let be the displacement equation of the individual waves that superimposed then the displacement of the resultant wave is :
*Thank You*



Post a Comment